Lineal-/Bleistiftmethode
Aus Unterrichtsmaterial
Version vom 14. April 2022, 16:11 Uhr von Yanflei (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „'''Die Lineal-/Bleistiftmethode:''' Die Lineal-/Bleistiftmethode wird angewandt um bei der Arbeit mit Datenkarten und der Suche nach einem geeigneten Schwelle…“)
Die Lineal-/Bleistiftmethode:
Die Lineal-/Bleistiftmethode wird angewandt um bei der Arbeit mit Datenkarten und der Suche nach einem geeigneten Schwellenwert systematisch vorzugehen und die Schwellenwertsuche visuell zu unterstützen. Das ganze funktioniert wie folgt:
- Die betreffenden Datenkarten werden aufsteigend nach einem Merkmal sortiert (bei zu vielen Karten ggf. 2 Tische aneinanderschieben)
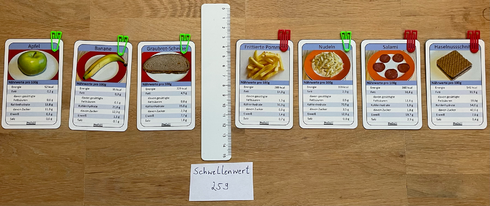
- Ein Lineal oder Bleistift wird als symbolischer Schwellenwert in die Verteilungen gelegt (zwischen zwei Karten) und dann wird ausgezählt, wie viele Karten richtig klassifiziert sind. Es wird auf beiden Seiten der Mehrheitswert gebildet (in der Abb.: links grün & rechts rot) und abweichende Karten gelten als falsch klassifiziert (hier: Nudeln auf der rechten Seite)
Schwellenwert per Augenmaß:
Um mit Hilfe der Linealmethode nicht alle möglichen Schwellenwerte ausprobieren zu müssen empfiehlt es sich etwas mit Augenmaß zu arbeiten, das einserseits durch Erfahrung aufgebaut wird aber auch durch folgende Hinweise unterstützt werden kann:
- Man kann einen ersten Schwellenwert per Augenmaß auswählen, um von da ausgehend verschiedene zu vergleichen. Die Karten müssen dafür auf jeden Fall nach einem Merkmal sortiert sein
- Es können verschieden Strategien genutzt werden:
- Es kann der Wert gewählt werden, der von links betrachtet zwischen den ersten beiden verschieden gelabelten Karten liegt (im Bild oben zwischen Brotscheibe und Pommes).
- Alternativ kann dies auch vom rechten Ende her gemacht werden.
- Alternativ kann ein Wert gewählt werden, bei dem links und rechts vom Schwellenwert möglichst homogene Teildatensätze (rot oder grün) entstehen. Dies erfordert schon ein größeres Augemaß, dass aber mit der Zeit aufgebaut werden kann.
- Von dem gewählten Schwellenwert ausgehend kann man dann den Schwellenwert etwas nach links oder rechts verschieben und prüfen, ob sich die Anzahl der falsch klassifizierten Karten dadurch verringert oder erhöht. Diese Strategie kann sukzessive nach links und rechts angewendet werden.
- So wird der beste Schwellenwert aus einer Menge betrachteter Schwellenwerte ermittelt. Alle Schwellenwerte zu testen (wie es ein Computer machen würde) ist bei einer großen Anzahl von Karten mühsam, aber mit Augenmaß und etwas ausprobieren kann man auch den besten Schwellenwert, gemessen an der Anzahl der Fehlklassifikationen, finden .